PROPOSICIÓN: DIVISIÓN ENTERA Y DIVISIÓN ENTERA DE POLINOMIOS

POLINOMIOS CLASES DÍAS 26 y 27/10

No tenía muy claro lo que era un polinomio, pero después de esta explicación sé perfectamente lo que es.

DISCUSIONES MATEMÁTICAS EN EL SIGLO XVI

Nuestro profesor nos pidió que leyéramos un artículo sobre Del Ferro, Tartaglia y Cardano. Pero antes de comenzar a hablar sobre las disputas de estos matemáticos durante el siglo XVI, os voy a hablar sobre algo muy curioso, ¿sabeis de dónde proviene la X?   Esa X que elevada al cubo, tantos dolores de cabeza les dio a estos tres matemáticos.

CURIOSIDAD

¿DE DÓNDE PROVIENE LA X?

En álgebra, el signo de ‘X’ a menudo se utiliza para representar una cantidad desconocida o variable. Del mismo modo, en inglés, la X también representa lo desconocido, como en losRayos X, que tanto desconcertaron a su descubridor; o como Malcolm X, que eligió el símbolo para representar el nombre olvidado de sus ancestros africanos.

Pero ¿de dónde viene exactamente la X? De muy lejos. Pero también de muy cerca. En el siglo XVI aC. los egipcios ya desarrollaron un álgebra muy elemental que usaron para resolver problemas cotidianos que tenían que ver con la repartición de víveres, de materiales…en una palabra de “cosas”.

Ya para entonces tenían un método para resolver ecuaciones de primer grado que se llamaba el “método de la falsa posición”. No tenían notación simbólica pero utilizaron el jeroglífico “hau”(que quiere decir “montón” o “pila”) para designar la incógnita. Sin embargo no fue hasta el siglo IX cuando esta incognita tomó la forma que hoy todos conocemos.

Es la epoca del matemático y astrónomo musulmán Al-Jwarizmi (Al-Juarismi), cuyas obras fueron fundamentales para el conocimiento y el desarrollo del álgebra. Su nombre latinizado dio origen a la palabra “algoritmo” y fue también cuando se acuñó el término “álgebra”, que deriva del título de su obra más importante, que presenta las reglas fundamentales del álgebra,Al-jabr wal muqabala.

Según la Wikipedia, el signo de X se remonta a esta época y a la palabra árabe que significa “cosa”, o “šay’ ” (شيء). En los textos antiguos, tales como el Al-Jabr, manuscrito que escribió en Bagdad en el 820 dC, las variables matemáticas se les llamaba “cosas” (en una ecuación se podía leer “tres cosas igual a 15″, con lo que la cosa tenía cinco años, por ejemplo).

Y ahí es donde entramos los españoles en contexto, pues fuimos los catalizadores de la X tal y como hoy la conocemos. Cuando el texto  de Al-Jabr fue traducido al español antiguo, la palabra “šay’ “se latinizó y se escribió como “xei”. Este término, por efectos prácticos, pronto se abrevió como simplemente….X.

Fue así como comenzó el hábito de utilizar letras para representar cantidades en álgebra.

TARTAGLIA, CARDANO Y DEL FERRO

RESUMEN DE LA HISTORIA

Ya aparecen resueltas ecuaciones de 2º grado en tablillas babilónicas de hace 4000 años. En el año 830 de nuestra era el matemático árabe Al Khowarizmi en un libro cuyo título ha dado lugar a la palabra "Algebra" resolvió todos los tipos de ecuaciones de 2º grado. Pero no se hicieron avances con las de 3º grado hasta el Renacimiento italiano. Scipione del Ferro (1465-1526) de la Universidad de Bolonia encontró una fórmula que resolvía ecuaciones de 3º grado o cúbicas de un determinado tipo, pero no hizo público su resultado y se lo legó a su discípulo Antonio del Fiore, éste retó públicamente a Niccolo Fontana (Tartaglia)(1499-1557) a resolver 30 problemas cada uno, todos los de Del Fiore se reducian a ecuaciones cúbicas del tipo que sabía resolver. Tartaglia, in extremis, encontró la fórmula que le permitieron resolver los problemas y ganó el reto. Entonces entra en juego Cardano (1501-1576)(personaje con una biografía fascinante que el mismo escribió) que le pide a Tartaglia que le transmita su fórmula, después de hacerse rogar accede, pero a condición de que no la revele. Sin embargo, Cardano comparte la fórmula con su discípulo Ludivico Ferrari (1522-1565)y entre los dos resuelven la ecuación cúbica general y Ferrari, además, decubre una fórmula para resolver las de 4º grado. Por otra parte Cardano se entera que la fórmula de la ecuación cúbica ya la había descubierto Del Ferro y.....

Cardano escribe:

Scipione del Ferro, de Bolonia, hace más de 30 años inventó esta regla y la comunicó a Antonio María del Fior, de Venecia, quien celebró un certamen con Nic- colò Tartaglia, de Brescia, lo que dio ocasión a que Niccolò por sí mismo la [re]descubriera, el cual me la dio a mí, suprimida la demostración, como consecuencia de mis ruegos. Pertrechado de este auxilio, busque la demostración por varios caminos, lo que fue muy difícil.

CONCLUSIÓN

Vivimos en una sociedad muy competitiva en la cual nos esforzamos por llegar a lo mas alto, por llegar a ser los mejores a costa de lo que sea y sin tener en cuenta a los demás.

Esto es lo que les paso a estos 3 grandes matemáticos del siglo XVI. Los 3 tenían un objetivo común, hallar la solución de la ecuación de tercer grado. Cada uno investigaba por su cuenta, a la vez que se carteaba con los demás (se enviaban problemas), de esta manera intentaban averiguar algo sobre lo que había descubierto el otro.

Al final, se consiguió descubrir la solución, ¿pero qué hubiera pasado si hubieran trabajado codo con codo, si hubieran cooperado entre todos para descubrir la solución?

Con esto nuestro profesor nos quiere transmitir que trabajar en grupo es algo positivo, aunque a nosotros nos parezca que no. Que los demás nos pueden llegar a enseñar muchas cosas y además, podemos llegar a resolver problemas mas rápidamente al poner en común las ideas y los conocimientos de todos.

HE SACADO LA INFORMACIÓN DE ESTAS 2 PÁGINAS POR SI A ALGUIEN LE INTERESA PROFUNDIZAR EN ESTE TEMA:

DISPUTAS MATEMÁTICAS S XVI DEL FERRO, TARTAGLIA Y CARDANO

CARDANO Y TARTAGLIA

También he encontrado un libro en el que puedes seguir la entretenida historia del descubrimiento de la ecuación de tercer grado y la vida de sus protagonistas. Os dejo aquí abajo el link donde podéis encontrar la reseña del libro: Cardano y Tartaglia la aventura de la ecuacion cúbica

EJERCICIO DEL 23/10 SOBRE POLINOMIOS

Polinomios

Un polinomio es así: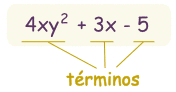

un ejemplo de polinomio este tiene 3 términos

Están hechos de (expresión algebraica formada por):

	constantes (como 3, -20, o ½)
	variables (como x e y)
	exponentes (como el 2 en y2) pero sólo pueden ser 0, 1, 2, 3, ... etc

Que se pueden combinar usando:

+ - ×	sumas, restas y multiplicaciones...
	... ¡pero no divisiones!

¿Son polinomios o no?

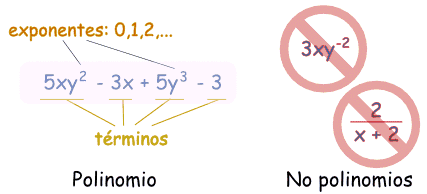
Estos  son polinomios:

• 3x
• x - 2
• 3xyz + 3xy²z - 0.1xz - 200y + 0.5

Y estos no son polinomios

• 2/(x+2) no lo es, porque dividir no está permitido
• 3xy^-2 no lo es, porque un exponente es "-2" (los exponentes sólo pueden ser 0,1,2,...)

Pero esto sí está permitido:

• x/2 está permitido, porque también es (½)x (la constante es ½, o 0.5)
• también 3x/8 por la misma razón (la constante es 3/8, o 0.375

Monomios, binomios, trinomios

Hay nombres especiales para los polinomios con 1, 2 o 3 términos:

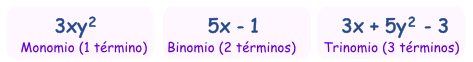
¿Cómo te aprendes los nombres? ¡Piensa en bicicletas!

(También existen cuatrinomio (4 términos) y quintinomio (5 términos), pero se usan poco) 

Muchos términos

Los polinomios pueden tener montones de términos, pero no infinitos términos.

¿Qué tienen de especial los polinomios?

Por su definición tan estricta, es fácil trabajar con polinomios.

Por ejemplo sabemos que:

• Si sumas o restas polinomios te sale un polinomio
• Si multiplicas polinomios te sale un polinomio

Así que puedes hacer muchas sumas y multiplicaciones con ellos, y siempre sale un polinomio al final.

Grado

El grado de un polinomio con una sola variable es el mayor exponente de esa variable.

Ejemplo:

El grado es 3 (el mayor exponente de x)

Para casos más complicados, lee Grado (de una expresión).

REPASO SOBRE INTERVALOS Y ENTORNOS

 Ya hemos terminado el tema 1, y no os he hablado nada sobre los intervalos y los entornos. Así que, aquí va un repaso sobre intervalos y entornos .

COMENTARIO SOBRE EL ARTÍCULO: BEYOND THE CLASSROM

Hoy os voy a hablar sobre un artículo que nuestro profesor de matemáticas, nos pidió que leyéramos hace unos cuantos días.

El artículo habla sobre un grupo de estudiantes americanos, a los que las clases de matemáticas no les aportaban lo suficiente. Por lo que decidieron cambiar la metodología de las clases, añadiendo trabajos en grupo, experimentación, auto aprendizaje al buscar las cosas por sí mismos…

El resultado de dicho experimento fue muy satisfactorio, ya que los alumnos afirmaban haber aprendido muchísimo más que por los métodos tradicionales.

Yo creo que con esto nuestro profesor, nos quiere hacer ver que no nos tenemos que ceñir sólo a lo que pone en los libros (que en algunos casos resulta aburrido y pesado). Tenemos que investigar por nosotros mismos, innovar y desarrollar nuevas formas de aprendizaje, ya que nos pueden resultar mucho más útiles y efectivas de lo que creemos. Nuestro profesor es un pionero en esta nueva forma enseñar.

Aquí está el enlace por si a alguien le interesa leer el artículo completo:

BEYOND THE CLASSROM/NUEVAS FORMAS DE APRENDER

Os recomiendo que le echéis un vistazo porque me ha parecido muy interesante.
¡PINCHA EN EL LINK DE ARRIBA!

¿RACIONALIZAR O DIVIDIR?/COMO RACIONALIZAR

 Hoy en clase,  José Ramón nos ha explicado la diferencia entre dividir un radical o racionalizarlo. 

 Aquí os explico, como racionalizar, en los distintos casos que os podéis encontrar. 

CLASE DÍA 19

La clase consistió en afianzar conceptos ya explicados y profundizar en las TERNAS PITAGÓRICAS.

 José Ramón nos pregunto si se cumpliría la siguiente proposición de la forma RECÍPROCA.

NÚMEROS RADICALES, ALGEBRAICOS Y TRANSCENDENTES

NÚMERO ALGEBRAICO

Un número algebraico es: cualquier número que es solución de un polinomio no nulo con coeficientes racionales.

Por decirlo más fácilmente, si tienes un polinomio como (por ejemplo):

2x²-4x+2 = 0

Entonces x es algebraico.

Porque:

• El polinomio no es cero
• x es un a raíz o cero (o sea, x da el resultado cero en la función 2x²-4x+2)
• los coeficientes son números racionales

El polinomio puede ser más simple o complicado que este ejemplo, claro, mientras los coeficientes sean racionales.

Propiedades

El conjunto de números algebraicos es numerable.

Todos los números racionales son algebraicos, pero un número I irracional puede ser o no algebraico.

¿POR QUÉ Φ  ES ALGRBRAICO?

Φ FI ES ALGEBRAICO porque es la solución de una ecuación polinómica cuyos coeficientes son números racionales.

NÚMEROS TRANSCENDENTES

Un número transcendente es un número que no es un número algebraico (es decir, no es solución de ninguna ecuación polinómica con coeficientes racionales).

Algunos ejemplos de números transcendentes son π y e

Números de Liouville

Ya en 1844, Joseph Liouville estudió este número:

	= 0,11000100000000000000000100……
	(cada cifra es 1 si está n! posiciones después del punto decimal, y 0 si no.)

Es un número muy interesante porque:

• es irracional, y
• además no es solución de ninguna ecuación polinomial así que no es algebraico.

De hecho, Joseph Liouville acababa de encontrar el primer número transcendente que se podía demostrar que lo era.

Ese número se conoce ahora como la constante de Liouville. Y es un número de Liouville.

Más números transcendentes

Hubo que esperar hasta 1873 para el primero número "no construido" que fuera transcendente, cuando Charles Hermite demostró que e es transcendente.

Después en 1884, Ferdinand von Lindemann publicó una prueba de que π es transcendente.

De hecho, demostrar que un número es transcendente es bastante difícil, aunque se sepa que son muy comunes...

Los números transcendentes son comunes

Casi todos los números reales son transcendentes. El argumento para verlo es:

• Los números algebraicos son "numerables" (por decirlo simplemente, la lista de números enteros es "numerable", y puedes ordenar los números algebraicos para que vayan de par en par con los números enteros, así que también son numerables.)
• Pero los números reales no son "numerables".
• Y como cada número real es algebraico o transcendente, los transcendentes deben ser "no numerables".
• Así que hay muchos más transcendentes que algebraicos.

Funciones transcendentes

Así como un número transcendente "no es algebraico", una función transcendente también es "no algebraica". Más formalmnte, una función transcendente es una función que no se puede construir en un número finito de pasos a partir de las funciones elementales y sus inversas, por ejemplo la función seno Sin(x).

Ejemplo: ¿√2 (la raíz cuadrada de 2) es algebraico o transcendente?

√2 es una solución de x² - 2 = 0, así que es algebraico

PROPOSICIONES MATEMÁTICAS Y LEYES DE DE MORGAN

Al principio cuando José Ramón nos explico las proposiciones, no le dimos mucha importancia (yo por lo menos), después de un mes de clase, me he dado cuenta de que las proposiciones sirven para todo en matemáticas. Por lo que tenía que crear una entrada explicando en que consisten.

¿Qué es una proposición matemática?

Una proposición matemática  p es un contenido semántico al que se le asigna uno de dos posibles valores de verdad: V (verdadero) F (falso)

* no (no p) = p

PROPOSICIÓN DE TIPO IMPLICACIÓN Y PROPOSICIONES RELACIONADAS

=>IMPLICACIÓN:      p        q

Se lee p implica q o también si p entonces q.

p es la hipótesis y q es la tesis, también se dice que p es condición suficiente para q y q es condición necesaria para p.

-Si una proposición es verdadera se debe realizar una demostración. 

-Si una proposición es falsa se debe realizar un contraejemplo.

Leyes de De Morgan:

Son una parte de la lógica preposicional y analítica, fueron creadas por Augustus de Morgan.

1-  ¬(P ^ Q) = (¬P v ¬Q) 

2-  ¬(P v Q) = (¬P ^ ¬Q)

VIDEO INTERESANTE SOBRE LAS LEYES DE DE MORGAN: LEYES DE DE MORGAN

TEORÍA DE CONJUNTOS

Uno de los primeros días de clase estuvimos hablando sobre la TEORÍA DE CONJUNTOS, hoy os voy a hablar un poquito sobre ello ya que me parece un tema muy interesante.

Idea de conjunto

Todos tenemos la idea de lo que es un conjunto: es una colección, agrupación, asociación, reunión, unión de integrantes homogéneos o heterogéneos, de posibilidades reales o abstractas. Los integrantes pueden ser números, letras, días de la semana, alumnos, países, astros, continentes, etc. a estos integrantes en general, se les denomina "elementos del conjunto".

Definición de conjunto

"La presencia o ausencia de elementos con características semejantes dentro de un contexto real o imaginario".

NOTACIONES DE UN CONJUNTO

 A  los conjuntos se les denotará con letras mayúsculas A, B, C…..y a sus elementos con letras minúsculas; a, b, c, d,…...para separar los elementos se emplean comas (,) y el punto y coma (;) para separar conjuntos o subconjuntos. Cuando un conjunto "P" está constituido por varios elementos como por ejemplo: a, b, c o por subconjuntos: {d, e}; los escribimos entre LLAVES "{}".

• Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î P.

• En caso contrario, si q no es un elemento de A se denota aÏ P.

Un conjunto se determina por extensión cuando se nombran todos sus elementos, y por comprensión cuando se da la característica común de sus elementos.

Ejemplos de conjuntos:  
 

• Æ : el conjunto vacío, que carece de elementos.
• N: el conjunto de los números naturales.
• Z: el conjunto de los números enteros.
• Q : el conjunto de los números racionales.
• R: el conjunto de los números reales.
• C: el conjunto de los números complejos.
• U: el conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, este conjunto depende del problema que se estudia, algunas veces se representa con la letra S (espacio muestral).

Subconjuntos

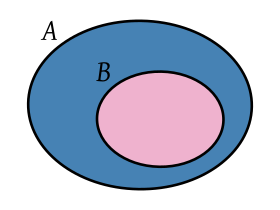
Sean los conjuntos A={ 0, 1, 2, 3, 5, 8 } y B={ 1, 2, 5 }

En este caso decimos que B esta contenido en A, o que B es subconjunto de A. En general si A y B son dos conjuntos cualesquiera, decimos que B es un subconjunto de A si todo elemento de B lo es de A también.

Por lo tanto si  B es un subconjunto de A se escribe B Ì A. Si B no es subconjunto de A se indicará con una diagonal Ë .

Operaciones con conjuntos

Diagramas de Venn

Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.

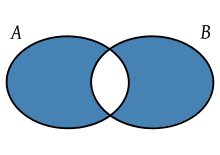
UNIÓN: de dos conjuntos A y B al conjunto formado por objetos que son elementos de A ó de B, es decir:

A È B := { x | x Î A Ú x Î B}.

INTERSECCIÓN: de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B, es decir:

A Ç B := {x | x Î A Ù x Î B}.

CONJUNTO VACIO: Un conjunto que no tiene elementos es llamado conjunto vacío ó conjunto nulo lo que denotamos por el símbolo Æ .
A Ç B= { }  muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:
A Ç B=Æ

COMPLEMENTO: El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' y que se representa por comprensión como:

A'={ x Î U/x y x Ï A }

Verifican las siguientes propiedades:

• A È Æ = A , A Ç Æ = Æ ( elemento nulo ).
• A È U = U , A Ç U = A ( elemento universal ).
• ( A È B )' = A' Ç B' , ( A Ç B )' = A' È B' ( leyes de De Morgan ).

*En la siguiente entrada hablaré sobre la lógica matemática, ya que está estrechamente relaciona con la teoría de conjuntos.

DIFERENCIA: Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprensión como:
A - B={ x/x Î A ; X Ï B }

 DIFERENCIA SIMÉTRICA: La diferencia simétrica de dos conjuntos A y B es el conjunto formado por los elementos de (A-B) y los elementos de (B-A). Se denota A ∆ B.

Es decir, A ∆ B = (A-B) È (B-A).

A ∆ B ={ x/x Î A y x Î B pero x Ï A Ç  B }