TEORÍA DE CONJUNTOS

Uno de los primeros días de clase estuvimos hablando sobre la TEORÍA DE CONJUNTOS, hoy os voy a hablar un poquito sobre ello ya que me parece un tema muy interesante.

Idea de conjunto

Todos tenemos la idea de lo que es un conjunto: es una colección, agrupación, asociación, reunión, unión de integrantes homogéneos o heterogéneos, de posibilidades reales o abstractas. Los integrantes pueden ser números, letras, días de la semana, alumnos, países, astros, continentes, etc. a estos integrantes en general, se les denomina "elementos del conjunto".

Definición de conjunto

"La presencia o ausencia de elementos con características semejantes dentro de un contexto real o imaginario".

NOTACIONES DE UN CONJUNTO

 A  los conjuntos se les denotará con letras mayúsculas A, B, C…..y a sus elementos con letras minúsculas; a, b, c, d,…...para separar los elementos se emplean comas (,) y el punto y coma (;) para separar conjuntos o subconjuntos. Cuando un conjunto "P" está constituido por varios elementos como por ejemplo: a, b, c o por subconjuntos: {d, e}; los escribimos entre LLAVES "{}".

• Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î P.

• En caso contrario, si q no es un elemento de A se denota aÏ P.

Un conjunto se determina por extensión cuando se nombran todos sus elementos, y por comprensión cuando se da la característica común de sus elementos.

Ejemplos de conjuntos:  
 

• Æ : el conjunto vacío, que carece de elementos.
• N: el conjunto de los números naturales.
• Z: el conjunto de los números enteros.
• Q : el conjunto de los números racionales.
• R: el conjunto de los números reales.
• C: el conjunto de los números complejos.
• U: el conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, este conjunto depende del problema que se estudia, algunas veces se representa con la letra S (espacio muestral).

Subconjuntos

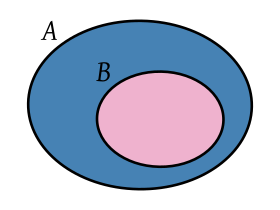
Sean los conjuntos A={ 0, 1, 2, 3, 5, 8 } y B={ 1, 2, 5 }

En este caso decimos que B esta contenido en A, o que B es subconjunto de A. En general si A y B son dos conjuntos cualesquiera, decimos que B es un subconjunto de A si todo elemento de B lo es de A también.

Por lo tanto si  B es un subconjunto de A se escribe B Ì A. Si B no es subconjunto de A se indicará con una diagonal Ë .

Operaciones con conjuntos

Diagramas de Venn

Los diagramas de Venn que de deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.

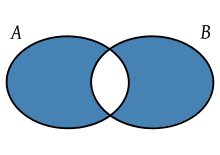
UNIÓN: de dos conjuntos A y B al conjunto formado por objetos que son elementos de A ó de B, es decir:

A È B := { x | x Î A Ú x Î B}.

INTERSECCIÓN: de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B, es decir:

A Ç B := {x | x Î A Ù x Î B}.

CONJUNTO VACIO: Un conjunto que no tiene elementos es llamado conjunto vacío ó conjunto nulo lo que denotamos por el símbolo Æ .
A Ç B= { }  muestra que no hay elementos entre las llaves, si este es el caso se le llamará conjunto vacío ó nulo y se puede representar como:
A Ç B=Æ

COMPLEMENTO: El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' y que se representa por comprensión como:

A'={ x Î U/x y x Ï A }

Verifican las siguientes propiedades:

• A È Æ = A , A Ç Æ = Æ ( elemento nulo ).
• A È U = U , A Ç U = A ( elemento universal ).
• ( A È B )' = A' Ç B' , ( A Ç B )' = A' È B' ( leyes de De Morgan ).

*En la siguiente entrada hablaré sobre la lógica matemática, ya que está estrechamente relaciona con la teoría de conjuntos.

DIFERENCIA: Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprensión como:
A - B={ x/x Î A ; X Ï B }

 DIFERENCIA SIMÉTRICA: La diferencia simétrica de dos conjuntos A y B es el conjunto formado por los elementos de (A-B) y los elementos de (B-A). Se denota A ∆ B.

Es decir, A ∆ B = (A-B) È (B-A).

A ∆ B ={ x/x Î A y x Î B pero x Ï A Ç  B }